The examples promised

Now, I have prepared samples of what we talked about three posts ago. I scanned two images, each with several examples covered. Figure 1 has examples 1-10, and figure 2 has examples 11-14.   Figure 1

 

Figure 2

 

In ex. 1, I have drawn a straight line. What is true of a straight line? There is much of a dynamic to it, is there? I believe that art gains power from dynamics and depth. In a straight line by itself, we aren't saying much, not there is no use for a straight line. Everything has a beginning, and a straight line is a good place to start when beginning to draw.

Ex. 2 shows an angle with a sharp corner. There is how a straight line begins to show a dynamic: simply by moving in a different direction. This is the beginning of the concept of motion in art: an angle.

Ex. 3 shows a curve. it is somewhat like the angle, but it is rounded and soft in its change of direction, giving it a softer and less sudden dynamic.

Ex. 4 shows a circle, a two-dimensional shape, which means it has height and width. So far, not very exciting, but it is very useful, as we will see in our journey, because organic shapes are filled with circular movement. The circle is also the parent of the sphere, which we will examine later.

Ex. 5 shows an ellipse, or an oval. It is, dynamically speaking, akin to the circle, yet flattened. It can also be stood on end and it would be said to be thinned, I believe. At any rate, an oval can be said to be an elongated circle.

Ex. 6 is a triangle. In our example, it is not equidistant on all sides, but only on two, having an elongated dynamic. The baseline of the triangle is much shorter than the two that are equal to one another, somewhat like a spire on a church.

Ex. 7 Here we have a square, which dynamically speaking is to the cube as the circle is to the sphere; it is the parent shape. It is made up of two equal right angles and has four corners.

Next, in ex. 8, we have the rectangle, which is, primarily, an elongated square.

Ex. 9 show a trapezoid that is made up of two non-equidistant lines and two curved lines on either side. There is another type of trapezoid that is similar, containing no curves and is comprised of all straight lines.

Ex. 10 brings to the final example on Figure 1, and this is the parallelogram. It is like unto a rectangle, but the difference lies in that the rectangle is slanted to one side.

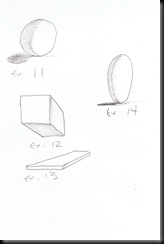
Looking to Figure 2, we have a few three dimensional shapes. In ex. 11, we have a sphere, which as we learned earlier, is begotten of the circle. Here we begin, in our journey, applying illusory techniques to give the appearance of depth. When making two-dimensional art, we use highlighting or shading to give the illusion of light or shadow or depth, or any combination there of, or in other words, we are striving to make a two-dimensional work look three-dimensional.

In the next example, ex. 12, we have a cube-like shape that is borne of a square and two parallelograms. It is called, if you were to hold one in the natural world, a hexahedron, but in the virtual world of art, we, when working in only two dimensions, we will look at it as a triplanar shape, a mass comprised of the different planes. It is not the most complex of shapes, but is still a member of the polyhedron family.

Ex. 13 is similar to ex. 12, only it is representative of a flattened hexahedron, a board-like object.

And finally we have the egg-shaped example in ex. 14. I will call it an ovoid sphere, until either I am corrected , or until I stumble onto a truer designation in regards to nomenclature. Is is somewhat spherical, but unlike the sphere, it is not perfectly round/circular in genesis.

Here we have the inception of Project Everest, as I spoke of a few posts ago. I am going to blog my artistic progress as I (hopefully) improve and refine my draughtsmanship, the art of drawing. Talk to you soon.

 

Jasz